电工电路 电源等效法和戴维宁
功率等效换算过程如下。
即I=-44/(4+6)=-4.4(A)。
本质上,您获得了电源的等效转换。
在最后一张图中可以看到戴维宁等效电路参数:Uoc=-44V,Req=4Ω。
直接使用戴维南定理。
从电路中断开电阻 R=6Ω。
I1=(140+90)/(20+5)=9.2(A),Uoc=Uab=5×I1-90=5×9.2-90=- 44V。
或:Uoc=Uab=-20I1+140=-20×9.2+140=-44(V)。
电压源短路:Req=Rab=20∥5=4(Ω)。
I=Uoc/(Req+R)=-44/(4+6)=-4.4(A)。
计算出等效电源
1 解:设端口的顶节点和底节点为a和b。
假设2欧姆电阻的电流为I1,方向向上。
根据KCL,4欧姆电阻的电流为:(I1+1),方向向下。
根据KVL:2I1+4×(I1+1)=12,解:I1=4/3(A)。
所以,4欧姆电阻的电压为:U1=4×(I1+1)=4×(4/3+1)=28/3(V),正向上,负向下。
同样,假设3欧姆电阻的电流等于I2,方向向下,则根据KCL,6欧姆电阻的电流等于:I2-1,则方向是向上。
KVL:3I2+6×(I2-1)=12,I2=2(A),所以3欧姆电阻的电压为:U2=3I2=3×2=6(V) ,上正。
向下负。
所以:Uab=U1-12+U2=28/3-12+6=10/3(V)。
等效电阻:电压源短路,电流源开路,可得:Rab=2∥4+3∥6=4/3+2=10/3(欧姆)。
2. 令左侧 2 欧姆电阻的电流等于 I,且方向向上。
利用KSL可以得到各电阻的电流如下图所示:
通过KVL:3I+2×(I-4)=8×(7 -I)+ 4×(3-I)。
解方程我们得到:I=76/17 (A)。
所以:Uab=-2I+4×(3-I)=-2I+12-4I=12-6I=12-6×76/17=-252/17(V)。
电压源短路,电流源开路:Rab=(2+4)∥(2+8)=6∥10=3.75(Ohm)。
求等效电源解法
原图①:
电压源等效电压Uoc=开路电压20Ⅴ
电压源等效内阻Req=10//10=5欧姆。
等效电路②:
闭合K后,电压表显示U=20×5/(5+5)=10V。
等效电源的电动势、内阻公式推导及闭合电路欧姆定理的“闭合”内涵
本文深入讨论了等效电源的电动势和内阻公式的推导,以及闭路欧姆定理的“闭路”内涵。首先,我们了解了等效电源的概念,包括串联等效和并联等效。
串联等效时,等效电动势等于各电源电动势之和,等效内阻等于各电源内阻之和。
并联等效涉及求解等效电动势和计算内阻。
内阻的计算比较复杂,必须结合欧姆闭路定理推导。
对于闭合电路中的欧姆定理,它包含多种表达式,其中最常见的是通过电路的总电阻与总电流之间的关系来描述。
本文通过闭路欧姆定理的表达式和并联电路的分流法则,证明了并联等效电动势和内阻的公式。
通过简单的数学推导,清晰地论证了并行等价原理。
为了更直观地理解并联等效,我们介绍了理想电压表的测量方法,即直接将等效电源连接到理想电压表两端,读取两端电压,间接得到电动机当量。
力量。
同样,本文通过比较闭路欧姆定理的不同表达式,更详细地解释了等效内阻的计算方法。
除了等效电源的理论推导外,本文还探讨了闭路欧姆定理的本质,即电流流过闭路时电势不改变,但电势增大,为位于过程组件之间。
这个解释揭示了“闭合”在电路分析中的重要性。
通过比较基尔霍夫第一定律和第二定律,我们可以更好地理解电路分析。
最后,通过对实际电路问题的分析,论证了欧姆闭路定理在解决多电源电路问题中的应用。
借助基尔霍夫定律,我们可以有效地求解电路中的电流分布,从而解决实际问题。
本文旨在通过详细的理论分析和实际案例分析,帮助读者深入理解等效电源电动势和内阻公式的推导,以及闭路欧姆定理的“闭路”内涵。
希望读者掌握这些知识后能够更加自信地解决相关电路分析问题。
电压源与电流源并联和串联分别等效为什么,急
当电压源和电流源并联时,电压不变,电流增加I=I1+I2+
当电压源和电流源并联时串联,电流不变,电压增大U=U1+ U2+
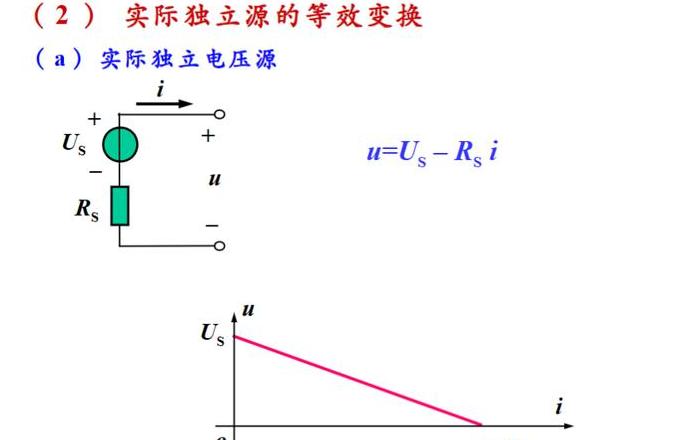
; 等效电源定理所谓“开路电压”是指:负载RL从电路中断开后a、b之间的电压,所谓“源去除”是指:假设电源; 去掉两端有源网络中的(恒压源短路,恒流源开路)。
对于复杂的电路,不可能用电阻串并联的方法来简化电路并求解,因此必须利用网络原理和定理来简化。
等效功率定理是简化两端有源线性网络和分析电路的重要定理。
任何二端电路,无论其复杂程度如何,都称为二端网络,如果该二端线性网络内部含有电源,则称为有源二端线性网络;
等效电源定理表述为:任何二端有源线性网络其外部电路总可以用等效电源模型代替。
由于电源模型分为电压源模型和电流源模型两种,因此有两种等效的电源定理,一种称为戴维南定理,另一种称为诺顿定理。
扩展信息
1 并联电路:并联电路允许电流在形成并联的电路元件之间采用多个独立路径。
它是两种基本方式之一的复合电路。
对于串联和并联电路,绘制物理电路的公式是:头连头、尾连尾、头进尾出。
2串联电路的电压规则
串联电路两端的总电压等于任意用电器件两端电压之和,
。>
这是:U=U1+U2
U1:U2:U3=IR1:IR2:IR3=R1:R2:R3
P1:P2:P3=IU1 :IU2:IU3=R1:R2:R3
串联电路的特点:
电流只有一条通路。
开关控制整个电路的通断。
每个电气设备都会相互影响。
串联电路中的电流处处相等:Itotal=I1=I2=I3==In
串联电路中的总电压等于各处的电压: 原始 U=U1+U2 +U3++Un
串联电阻的等效电阻等于各个电阻的总和: R 总计 = R1 + R2 + R3 + ? ? 个体功率:P总计 = P1 + P2 + P3 + ?+Pn [导数公式:P1P2/? (P1+P2)】
串联电容器的等效电容的倒数等于各个电容器的电容倒数之和:1/Ctotal=1/C1+1/C2++ 1/ Cn
串联电路中,除了电流处处相等外,其他所有物理量都成正比(串联电路也称为电路) 分压器):(电流所做的功是指同时做的功率的大小)R1:R2= U1:U2=P1:P2=W1∶W2=Q1∶Q2。
开关在任意位置控制整个电路,即其作用与其位置无关。
电流只有一条路径,通过灯泡的电流必须通过灯泡其他。
如果一盏灯熄灭,另一盏灯也必须熄灭。
在一个电路中,如果要控制所有电路,可以使用串联电路。
在串联电路中,只要有一部分断开,整个电路就变成开路。
也就是说,串联连接的电子元件无法正常工作。
参考来源:百度百科:串联与并联